Extended Nyquist Filters

Kok Chen, W7AY
February 23, 2012
Expanded: March 7, 2013


Introduction

In a 1928 paper, H. Nyquist described the necessary and sufficient conditions for a filter to pass a telegraph element without being subjected to intersymbol interference.

For a rectangular signaling pulse shape, the Nyquist filter which has the narrowest bandwidth is a Raised Cosine filter. However, in the absence of adjacent channel interference, the wider Matched Filter outperforms the Raised Cosine filter under Additive White Gaussian Noise (AWGN) conditions.

This paper describes an effective method for deriving other filters which obey the Nyquist criteria. For a rectangular pulse, these extended Nyquist filters have bandwidths that are in between the bandwidth of the Raised Cosine filter and the bandwidth of the Matched Filter.

The method described here can be used to derive Nyquist filters for other signaling pulse shapes.


Nyquist Criteria

In "Certain Topics in Telegraph Transmission Theory," Harry Nyquist introduced three conditions that are required for the reception of a telegraph signal without suffering from intersymbol interference (ISI). The first condition is that the amplitude of the filtered wave at the mid-bit sampling locations are constant and independent of the bit sequence. The figure below (taken from Figure 2 in Nyquist's paper) shows the transfer functions of filters that meet this condition:

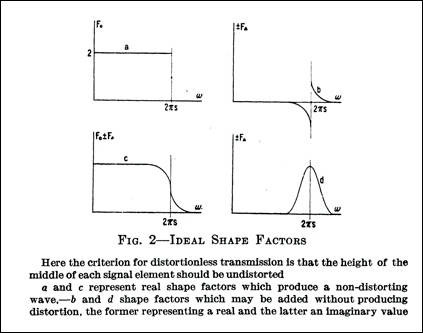
Figure 1 : (from Nyquist) First Nyquist Condition

In the figure, curve a is a transfer function that meets Nyquist's first criterion. Curve b represents a real function, and curve d represents an imaginary function (odd and even functions, respectively around ω = 2πs) that can be added to curve a to create a new transfer function, as exemplified by curve c in the figure, which continues to meet Nyquist's first criterion.

The second of Nyquist's conditions requires the period of the signaling elements to be constant, regardless of the actual bit sequence. The figure below (taken from Figure 3 in Nyquist's paper) shows the transfer functions that satisfy this condition.

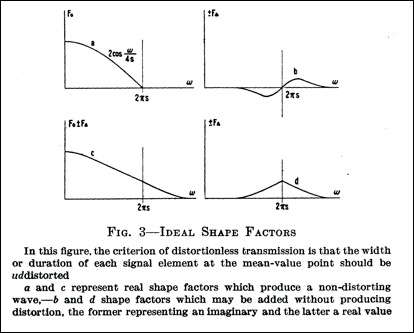
Figure 2 : (from Nyquist) Second Nyquist Condition

In this case, curve b is an imaginary term and curve d is a real term which can be added to curve a.

The third Nyquist criterion requires the area under the curve of the filtered pulses to be directly related to the magnitude of the transmitted pulse. This last property is seldom mentioned in the literature.

The transfer function of a filter that is free of ISI has to meet both the conditions that are shown in Figure 2 and Figure 3 in Nyquist's paper.


Raised Cosine Filter versus Matched Filter

As mentioned earlier, the Raised Cosine filter meets the Nyquist Criteria for an input that consists of rectangular pulses.

In the absence of adjacent channel interference, the filter that provides the best SNR in the Additive White Gaussian Noise (AWGN) channel is not the Raised Cosine filter, but instead is a Matched Filter. For the rectangular signaling pulse, the Matched Filter is simply a Finite Impulse Response (FIR) filter that has a rectangular kernel, with a length that is the same duration of the input pulse. The Matched Filter for a rectangular pulse can also be viewed as an integrate-and-dump detector.

The following figure shows the transfer functions of a Raised Cosine filter (β = 1) and a Matched Filter for the same rectangular pulse.

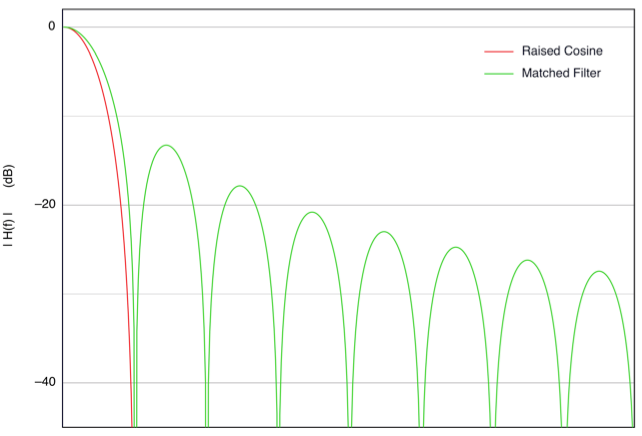
Figure 3 : Transfer Function for two Nyquist Filters

The next figure shows the performance difference between these two Nyquist filters when they are used in an FSK demodulator (5 bit Baudot).

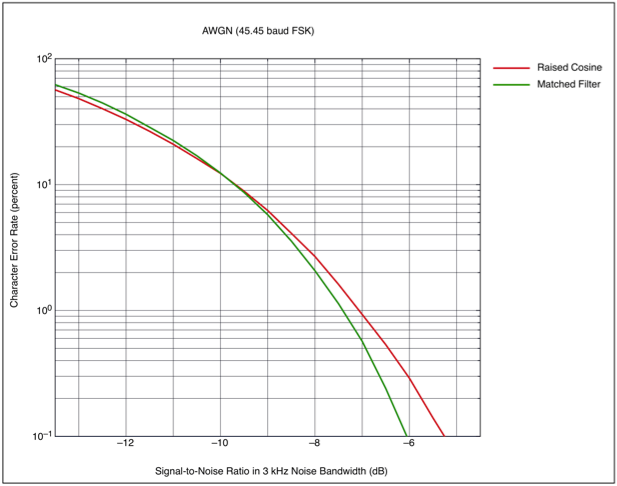
Figure 4 : FSK Error Rates

As shown above, the Matched Filter requires almost 0.5 dB less SNR to reach a 1% character error rate, and about 0.75 dB less SNR to reach a 0.1% error rate. The Matched Filter's main drawback is that it uses up a much wider bandwidth, thus more susceptible to adjacent channel interference.

The next figure shows a Raised Cosine filter that is too narrow (0.6 times and 0.8 times the proper bandwidth needed for baud rate) and thus producing intersymbol interference even when the SNR is good.

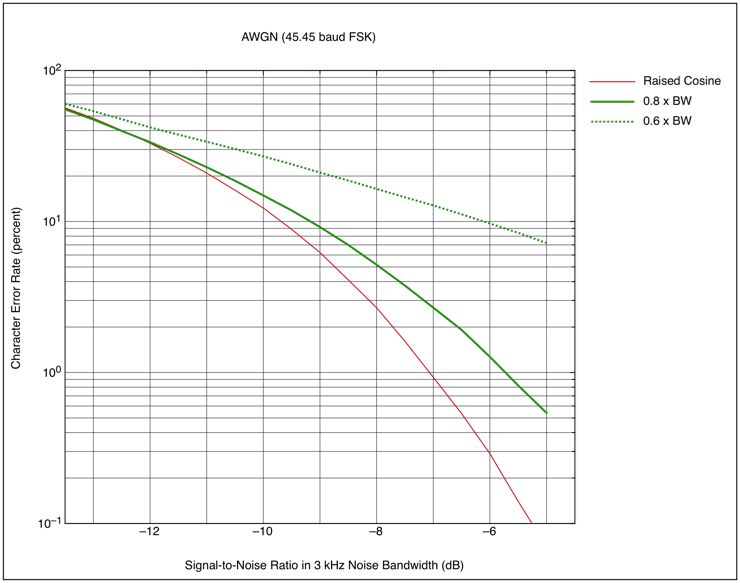
Figure 5 : FSK Error Rates for Raised Cosine with narrow Bandwidths

The following figure shows a Raised Cosine filter that is too wide (1.5 times and 3 times the proper bandwidth needed for baud rate) and thus including more noise.

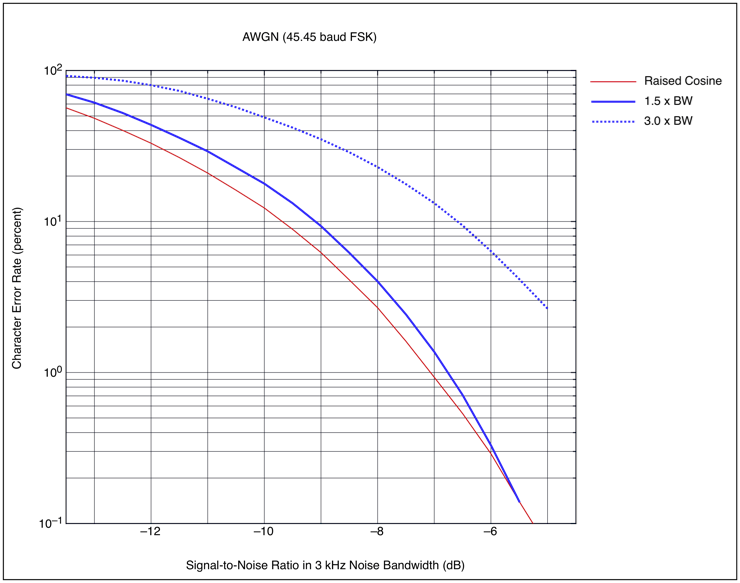
Figure 6 : FSK Error Rates for Raised Cosine with wide Bandwidths

Figures 5 and 6 illustrate that one cannot make the Raised Cosine perform any better by narrowing or widening its bandwidth.


Extending Nyquist Filters

Starting with a known Nyquist filter, we will now show how to obtain a family of filters which also satisfy the Nyquist criteria.

By starting with a Raised Cosine filter, the algorithm produces a sequence of a filters that approaches the Matched Filter in the limit.

Each filter in the sequence has successively wider bandwidth, but unlike the narrow and wider Raised Cosine filters mentioned earlier, this set of filters remains compliant with Nyquist's conditions. This allows one to choose better bandwidth tradeoffs.

Let us first regress on the Nyquist conditions. Nyquist filters implicitly guarantees the integrity of data values that are taken at mid-bit locations, whether the bit sequence consists of alternating bit, or alternating pairs of bit where the data remains constant every two bits. This is shown for a Raised Cosine filter in the following figure.

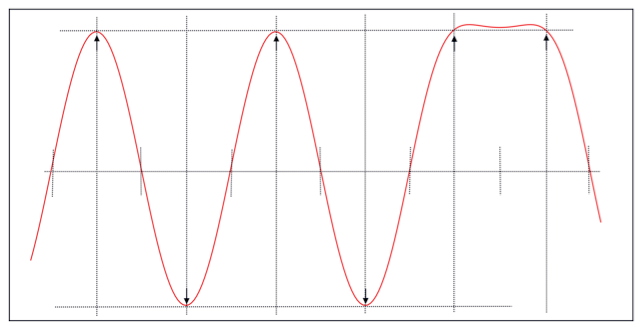
Figure 7 : Raised Cosine Filter Response

Even though there is some ripple from the filter's impulse response, notice that the sampling values for the last two samples are located at the same levels as the sample amplitudes for the isolated bits before it. This is Nyquist's first condition. The time offsets are fixed by Nyquist's second condition.

What this implies is that when a bit stream with bit period T is passed through a Nyquist Filter that is designed instead for a bit period of T/2 (i.e., a Nyquist filter that is exactly twice the bandwidth), the sampling values at 0.25T and 0.75T from the leading edge zero crossings are correct values.

Since the superposition of these two samples must also yield the correct sampling value, we can write the following recursion,

             [Equation 1]

In Equation 1, if h_N(t) is the impulse response of a Nyquist filter, then h_N+1(t) is an impulse response of a filter that also satisfy the Nyquist conditions.

By starting from a known Nyquist Filter h₀(t), we can therefore derive a family of Nyquist filters h₁(t), h₂(t), etc. Specifically, there is a family of Nyquist filters that starts with a Raised Cosine filter.

In C, this recursion can be written as


The extendedNyquistRecur() function returns a standard Raised Cosine kernel when n=1. The raisedCosine() function can be replaced by any other Nyquist filter.


Impulse Response of Extended Raised Cosine Filters

Starting with the impulse response h₀(t) of a Raised Cosine filter, Figure 8a shows the impulse responses of successive applications of Equation 1. h₁(t) is the second order extension (first recursion) of the Raised Cosine filter, h₂(t) is the third order extension (second recursion) of the Raised Cosine filter, etc.

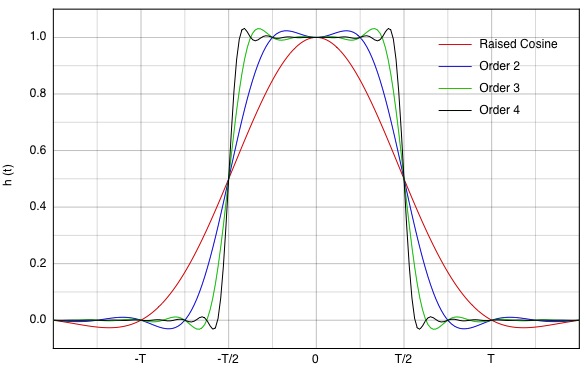
Figure 8a : Impulse Responses of "Extended Raised Cosine" Filters

The above shows the typical β=1 Raised Cosine for a baud rate of 1/T as having a zero impulse response at t=T. And, as the filter order increases, the impulse response appears to converge to a Matched Filter, which is a rectangle between (-T/2 and T/2).

Figure 8b shows the same plots in Figure 8a, expanded in the region of t=T, which is the sampling point of the next bit.

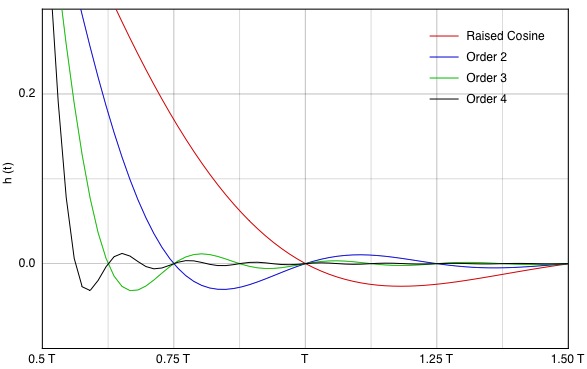
Figure 8b : Impulse Responses of "Extended Raised Cosine" Filters around t=T

It can be seen that for the basic Raised Cosine, ISI increases very rapidly when the baud rate is higher than the designed baud rate.



Transfer Function of Extended Raised Cosine Filters

Starting with the Fourier relationship



together with the Fourier Scaling theorem and Fourier Shift theorem,



and



the Fourier Transform of Equation 1 becomes

         [Equation 2]

With the Euler formula, the recursion simplifies to

                 [Equation 3]

The following figure shows the transfer functions from the first few applications of Equation 3:

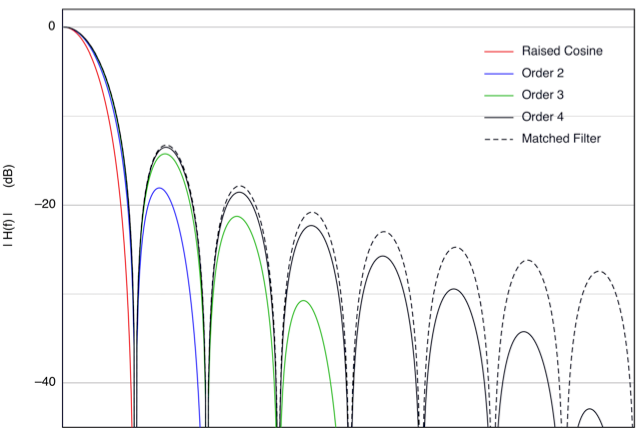
Figure 9 : Transfer Functions of "Extended Raised Cosine" Filters

Notice from Figures 8 and 9 that the sequence of extended Raised Cosine filters approaches the Matched Filter (rectangular impulse response and sin(x)/x transfer function).

Equation 3 also looks deceptively simple: a Nyquist filter results from another Nyquist filter of twice the bandwidth that is multiplied by a cosinusoidal function. In the next section, we shall see that this formulation is also very effective.


Performance of Extended Raised Cosine Filters

Figure 10 shows the character error rate when a 2nd order extended Raised Cosine filter is used in an FSK demodulator, together with character error curves for the fundamental Raised Cosine filter and the Matched Filter for comparison. Figure 11 shows the character error rate for a 3rd order extended Raised Cosine filter.

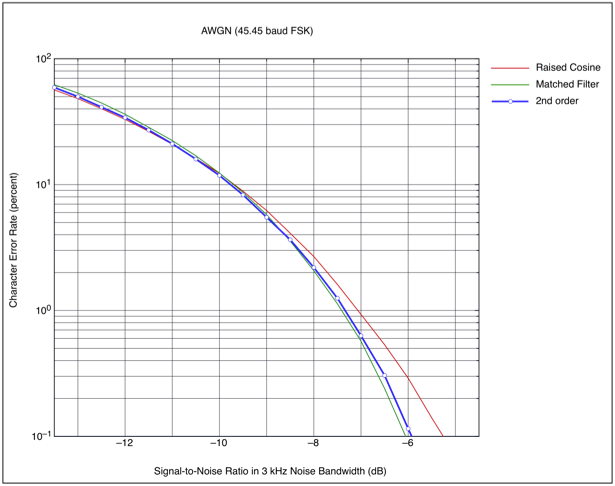
Figure 10 : FSK Error Rates for 2nd order extended Nyquist Filter




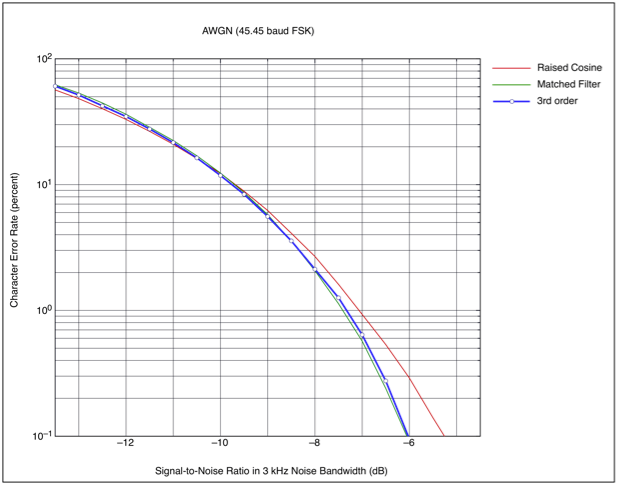
Figure 11 : FSK Error Rates for 3rd order extended Nyquist Filter

Notice that for practical purposes, the filter shown the Figure 10 is virtually equal to the performance of a Matched Filter. The third order filter in Figure 11 shows a very small improvement at the expense of a wider -30 dB bandwidth.




Frequency Domain Design

Notice from Figure 8 that the impulse response for all the filters have the same -6 dB width. However, the impulse responses do not all cross the y axis at 0



Conclusion

Starting from a known Nyquist filter, we have presented an effective recursive algorithm (Equation 1) to create a family of filters that satisfy the Nyquist criteria. For a Raised Cosine filter, the sequence of these "extended Nyquist filters" appear to converge to a Matched Filter, i.e., the impulse response of a filter in the sequence approaches a rectangle and the transfer function approaches a sin(x)/x function.

We further showed that even the first iteration of the algorithm, which has a much narrower bandwidth than the Matched Filter, comes very close to the performance of a Matched Filter when used as a data filter for FSK.


Reference

H. Nyquist, "Certain Topics In Telegraph Transmission Theory," AIEE Transactions, Vol 47, April 1928 pp 617-644.

• Extended Nyquist Filters