NC provides a data structure for describing and manipulating vectors in 3-dimensional space. These vectors can be used to describe wire geometries.
Just as int, real and element are keywords that are used to define integer, real and wire element variables, vector variables are defined using the keyword vector. Additionally, transformations to manipulate the vectors are defined with the keyword transform.
Vectors can be initialized by using the vect() function call. vect() takes three argument, the x, y and z components, respectively of the vector. The arguments are real or int variables, expressions or constants. For example:
- vect( 2.0, y, cos( angle ) )
Vectors can be scaled by int or real scalars; the following three expressions describe the same vector:
- 2.0*vect( x, y, z ), vect( x, y, z )*2.0, vect( x*2, y*2, z*2 )
You can add or subtract two vectors to form a third vector
- vector t, u, v ;
u = vect( 1, 2, 3 ) ;
v = vect( 4, 5, 6 ) ;
t = u + v ;
Negating a vector variable will create a vector whose components are negated.
Retrieving components of a vector object
You can extract the three components of a vector into real values by using the . (dot) operator followed by the character "x," "y" or "z." (i.e., as if x, y and z are structure members in the C language). The following will print "1.000 2.000 3.000" to the output console:
- vector v ;
real x, y, z ;
v = vect( 1, 2, 3 ) ;
printf( "%f %f %f\n", v.x, v.y, v.z ) ;
Transformations
NC transformations are affine transformations of the form:
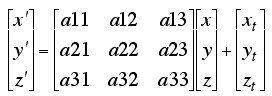
The (xt, yt, zt) vector is a constant vector to provide the translation term of the affine transform.The coefficients a11, a12,... a33 of the 3x3 matrix forms a rotation, reflection, shear or expansion and contraction of the vector (x, y, z). The following matrix rotates a vector around the z-axis:
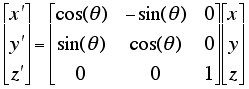
In NC, an affine transform is internally represented by a 4x4 augmented matrix.
The affine transformation is defined in NC by declaring a variable with a transform type. An identity matrix with no translation term, i.e.,
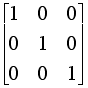
leaves the original (x, y, z ) components of a vector unchanged. In NC, this is generated by using the following system call:
- transform T ;
T = identityTransform() ;
A transformation operates on a vector by using the * (multiply) operator.
- transform T ;
vector v, u ;
v = vect( 1, 2, 3 ) ;
T = identityTransform() ;
u = T * v ;
Notice that in the above, the result u is also the vector ( 1, 2, 3 ) since we have multiplied the vector v by an identity matrix.
- Scaling
Like a vector, a transform object can be scaled by a scalar variable. Please note that the translation terms of the affine transform will also be scaled. For example, 2.15*identityTransform() represents an affine transform with the following matrix:

- Rotating
You create a transformation which rotates a vector by 10 degrees around the x-axis by using the rotateX system call:
- transform T ;
real angle ;
angle = 10.0 ;
T = rotateX( angle ) ;
Similarly, rotateY and rotateZ are system calls that rotate a vector around the y-axis and z-axis.
Concatenated Transformations
Concatenated transforms (matrix multiplication) are created by using the * operator between any two transform variables.
For example, if you define a new transformation T as
- T = rotateX( 15 )*rotateY( 40 ) ;
When applied to a vector (i.e., T*v) , the concatenated transform will first rotate the vector around the y-axis by 40 degrees and then rotate the result around the x-axis by 15 degrees.
Like matrix operations, an affine transform is not generally commutative (i.e., A*B is in general not the same as B*A).
When concatenating to an existing transform that has a translation term, the original translation will also be altered by the new transform. Only the translation terms of the last (leftmost) transform in a sequence of transform operations are left unchanged. Concatenating a new rotation transform (left multiply with a new transform) will rotate the translation terms of the original transform and add it to the translation term in the new transform. Refer to this page for the mechanism of an affine transform.
Translation Transformations
Notice that the transformations discussed so far have no translation term. A translation transform can be generated by using the following system call:
- transform T ;
vector v ;
v = vect( 0, 0, 11.0 ) ;
T = translateTransform( v ) ;
The above creates a translation transform object that will add 11 meters to the z component of a vector that the transform operates on.
- transform T ;
vector v ;
v = vect( 0, 0, 11.0 ) ;
T = translateTransform( v ) ;
S = T*rotateX( 30 ) ;
R = rotateX( 30 )*T ;
In the above example, S will first rotate a vector around the x-axis by 30 degrees and then translate the vector vertically by 11 meters, whereas R will first translate a vector vertically by 11 meters and then rotate it around the x-axis by 30 degrees. The last transform in a concatenated transform operates first on a vector.
Arbitrary Transformations
You can specify more general 3x3 matrices (for example, a shear matrix) for the affine transform by calling:
- T = transformWithMatrix( a11, a12, a13, a21, a22, a23, a31, a32, a33 ) ;
You can apply a translation term by premultiplying the transform with translateTransform( v ).
Retrieving components of a transform object
You can extract the 9 components of a matrix of an affine transformation by calling matrixElement( T, i, j ) where T is the transform object and i and j are integers which are the coefficients of Tij. (T,0,0) returns a11, (T,1,0) returns a12, (T,i,j) returns a(j+1)(i+1).
You can extract the translation term of an affine transform by calling translationElement( T, i ) where T is the transform object and i = 0 for the x component of the translation, i = 1 for the y component of the translation and i=2 is the z component of the translation.
Calling user functions with vector and transform objects
You can pass vector objects and tranform objects into a user function just as you pass integer, real and element variables. Similarly, functions can return vector and transform objects. For example:
- vector op( transform T, vector v )
{
- return = T*v ;
}
Creating wire structures using vector and transform objects
NC has the wire, line and taperedWire functions to specify geometry structures by using scalar numbers to specify coordinates. You can also describe wire geometries using vector variables. These are (please note that their names end with a "v"):
wirev( t, v0, v1, radius, segments )
linev( t, v0, v1, radius, segments )
taperedWirev( t, v0, v1, radius, sengmentLength0, segmentLength1 )
v0 and v1 are vectors that represent coordinates in 3-space. In addition to the vectors v0 and v1, the vector functions include a transform variable t . The affine transformation represented by t is applied to v0 and v1 before the resultant vectors are used to generate the actual coordinates for the wires. This allows you to rotate or move the wire element by just modifying the transform variable t.
The other variables in the vector version of the geometry functions are the same as their counterparts in the scalar versions of the functions.
The keyword nil can be used in place of the transform variable for the case where a transformation is not used. In this context, nil is equivalent to using identityTransform().
For example, the following model will place a horizontal dipole 12 meters up and pointed northeast.
- model( "example" )
{
- transform T ;
vector v ;
T = translateTransform( vect( 0, 0, 11.0 ) ) * rotateZ( 45 ) ;
v = vect( 0, 5.2, 0 ) ;
voltageFeed( wirev( T, v, -v, #14, 12 ), 1, 0 ) ;
}